We assume the particles are not interacting and that each particle has an equal probability to be anywhere in the box. Then the probability that a particle is within a volume
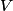 is is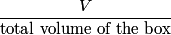 So, the probability that a particle is confined to a volume  is is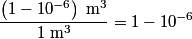 Because we assume that the particles are non-interacting, the probabilities for different particles are independent of one another, and so the probability that all of the particles are confined to a volume of  is is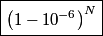 Hence, answer (C) is correct. |